To początek tego zadania. Myśle że mając ten podpunkt reszte zrobie sama ;)
Karola: Punkty A(−3,−1), B(1,2), C(2,5) są kolejnymi wierzchołkami równoległoboku ABCD.
a) Oblicz współrzędne wierzchołka D.
Założyłam ze odległosci wektorów AB i CD są te same. Odległość wektora wyszła mi 5, ale nie
wiem jak z tego wyliczyc wierzchołek D
Prosze o pomoc...
Eta:
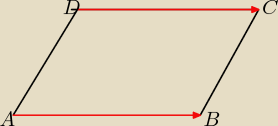
w równoległoboku:
→ → → →
AB = DC, AB= [4,3] , DC= [ 2−x
D, 5 −y
D]
2−x
D= 4 i 5−y
D= 3
x
D= −2 i y
D= 2
D( −2, 2)
Gustlik: Hmmmm. widziałem tego typu zadanie ostatnio rozwiązywane przez nauczycielkę w następujący
sposób:
1. Wyznaczone równanie prostej AB, oczywiście układem równań mimo istnienia prostszych metod,
2. J.w. równanie prostej BC.
3. Wyznaczone równanie prostej CD jako równoległej do AB (ten sam współcznnik kierunkowy) i
przechodzącej przez punkt C.
4. Wyznaczone równanie prostej AD jako równoległej do BC (ten sam współcznnik kierunkowy) i
przechodzącej przez punkt A.
5. Układ równań prostych AD i CD − z tego układu wyszły współrzędne punktu C.
Zapisana cała kartka formatu A4.
Metoda z Warszawy do Otwocka przez Paryż, Londyn, Nowy Jork, Buenos Aires, Tokio, Sydney i
Moskwę.
Oczywiście pokazałem tej dziewczynie metodę wektorową, taka jak pokazała Eta, okazało się, że
nauczycielka nie przerobiła wektorów, bo nie miała tego w programie, ale uczennica zakumała, o
co chodzi.
Ze wszystkich metod, jakie istnieją na rozwiązanie tego zadania nauczycielka wybrała
najdłuższą.
Nawet bez wektorów można było to zadanie rozwiązać prościej:
1. Wyznaczyc współrzędne środka ciężkości (S) równoległoboku jako środka przekątnej AC.
2. Mając wspołrzędne punktów B i S wyznaczyc współrzędne D.
A nawet rozwiązując równaniami prostych można było zrobić prościej − ominąć układy równań,
obliczyć same współczynniki kierunkowe AB i BC, bo do wyznaczenia prostych równoległych one w
zupełności wystarczą. I ze współczynnika kierunkowego AB wyznaczyc równanie prostej CD, a ze
wspólxczynnika BC − równanie prostej AD. Wprawdzie dłuższa metoda niż wektorowa czy ze środka
ciężkości, ale krótsza od metody tej nauczycielki. Tak wygląda nauczanie matematyki w polskich
szkołach. Boże − widzisz i nie grzmisz?
!
